IRL Experiment on Mountain Car
Overview
Inverse reinforcement learning deals with the case of learning the reward function for a situation or an activity where the optimum behavior is known.
Environment Details
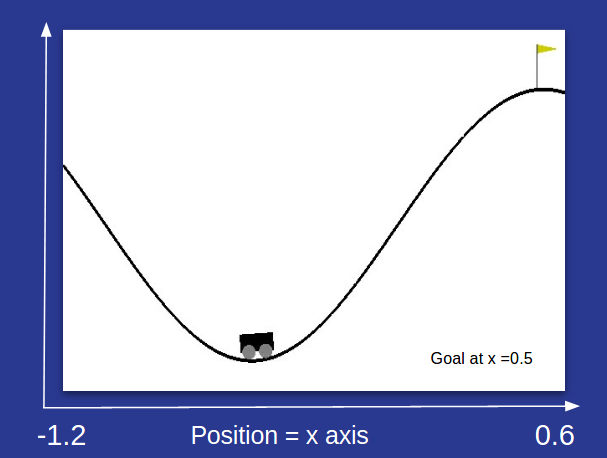
- Mountain car env : A car (agent) learning how to get to the top of the cliff in the least timesteps.
- The goal of the agent is to reach the goal position , represented by the flag at position = 0.5 units.
- The state space is a vector [position, velocity] with
- 1.2 ≤ position ≤ 0.6
- velocity∈[-0.07, 0.07]
- The above implies that the state space is continuous and infinite.
- The agent can perform 3 actions 0 ,1 ,2 :
- 0: accelerate in the left
- 1: zero acceleration
- 2: accelerate in the right
- Acceleration = 0.001 units
- The reward function inbuilt the environment is $R(s,a) = -1$ for each timestep and 0 if it reaches the goal.
Experiment Details
NG- Abbel paper vs Ours (Similarities)
- A linear function approximator for reward function with 26 basis functions.
- A penalty function with penalty constant = 2 in the updates of linear programming.
- Equally spaced Gaussian functions as their reward basis functions.
- Reward function depend only on the ‘position’ feature of state.
Differences:
- Test in the paper was a naive approach (Algo 2). While ours in Algo 3.
-
The paper discretized the state space $s= [position,~ velocity]$ into $120*120$ discrete states. This makes the number of states finite.
- They created a model based on the discretization of state space. We didn’t.
- They evaluated the Linear programming maximization for a bunch of 5000 states.
Results
- To be added